3 2018 Regular BECE Maths Paper 1
1. Which of the following is arranged in ascending order?
A. −25, −64, 4, 17
B. −64, −25, 4, 17
C. −64, −25, 17, 4
D. 17, 4, −25, −64
2. If P = {x: x is an even number greater than two and less than or equal to twelve}, list the members of P.
A. {2, 4, 6, 8, 10, 12}
B. {3, 4, 6, 8, 10, 12}
C. {2, 4, 6, 8, 10}
D. {4, 6, 8, 10, 12}
3. Which of the following is an infinite set?
A. {1, 2, …, 5, 6, 7}
B. {4, 6, 8, 10, 12}
C. {2, 3, 5, 7, 11, …}
D. {3, 6, …, 18, 21, …, 33, 36}
4. Find the HCF of 18, 36 and 60.
A. 22 × 32 × 5
B. 22 × 32
C. 2 × 3 × 5
D. 2 × 3
5. Write two hundred and two million, two thousand, two hundred and two in figures.
A. 202,002,202
B. 202,020,202
C. 202,022,202
D. 202,200,202
6. Find the number that can be added to 207 to make the sum divisible by 17.
A. 3
B. 13
C. 14
D. 30
7. If P = {factors of 36} and Q = {multiples of 4 less than 40}, find the number of subsets in P∩Q.
A. 10
B. 8
C. 6
D. 4
8. Find the LCM of 10, 15 and 25.
A. 90
B. 120
C. 150
D. 300
9. Evaluate \(\displaystyle \left( \frac23 - \frac14 \right) \div \frac56\)
A. \(\frac12\)
B. \(\frac{12}{25}\)
C. \(\frac{5}{12}\)
D. \(\frac15\)
10. Arrange \(\displaystyle \frac23, \frac49\) and \(\displaystyle \frac37\) in ascending order.
A. \(\frac23, \frac37, \frac49\)
B. \(\frac49, \frac37, \frac23\)
C. \(\frac37, \frac23, \frac49\)
D. \(\frac37, \frac49, \frac23\)
11. Find the simple interest on GHC 600.00 saved for 2 years 8 months at 5% per annum.
A. GHC 64.00
B. GHC 80.00
C. GHC 84.00
D. GHC 92.00
12. The number of girls in a mixed school is 420. If the ratio of boys to girls in the school is 3:2, how many students are in the school?
A. 1050
B. 1470
C. 1630
D. 1680
13. Mary had a chance to select a number from 1 to 20 randomly. What is the probability that the number is divisible by 3?
A. \(\frac{3}{20}\)
B. \(\frac15\)
C. \(\frac{3}{10}\)
D. \(\frac{7}{20}\)
14. Ama bought a pair of sandals for GHC 20.00 and sold it at GHC 24.00. Find her percentage profit.
A. 4%
B. 17%
C. 20%
D. 44%
15. Eight men can do a piece of work in 12 days. How long will 6 men take to do the same work if they work at the same rate?
A. 14 days
B. 16 days
C. 18 days
D. 20 days
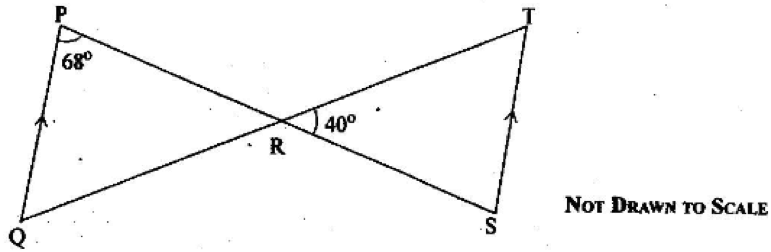In the diagram \(\overline{QP}\) is parallel to \(\overline{ST}\) angle QPR = 68° and angle SRT = 40°.
Use the information to answer questions 16 and 17.
16. Find the value of angle PQR.
A. 40°
B. 68°
C. 72°
D. 108°
17. Find the value of angle TSR.
A. 40°
B. 68°
C. 72°
D. 112°
18. A train is travelling at a speed of 60 km/h. What distance would it cover from 10:45 am to 12:15 pm?
A. 75 km
B. 87 km
C. 90 km
D. 150 km
19. The perimeter of a rectangle is 26 cm. If its length is 10 cm, find its area.
A. 30 cm2
B. 60 cm2
C. 130 cm2
D. 160 cm2
20. Find the slope of the line 3x - 6y = 33.
A. −3
B. \(-\frac12\)
C. \(\frac12\)
D. 3
21. If y = c + bx2, find y when \(c = \frac{14}{5}, b = \frac45\) and x = 2.
A. 3
B. 4
C. 6
D. 7
22. The volume of a cylinder is 20π cm3. If the height of the cylinder is 5 cm, find the base radius.
A. 1 cm
B. 2 cm
C. 3 cm
D. 4 cm
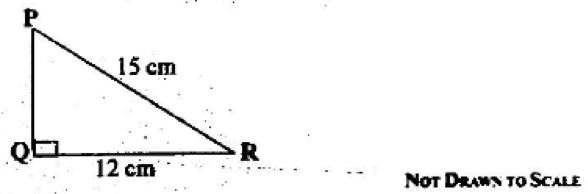
23. In the diagram, PQR is a right-angled triangle with |PR| = 15 cm and |QR| = 12 cm. Find the length PQ.
A. 3.0 cm
B. 8.0 cm
C. 9.0 cm
D. 19.2 cm
24. How many edges has a triangular prism?
A. 3
B. 5
C. 6
D. 9
25. Make m the subject of the relation \(q = \frac13 (m + n)h\).
A. \(m = \frac{3q}{h} - n\)
B. \(m = 3q - hn\)
C. \(m = 3q + hn\)
D. \(m = \frac{3q}{h} + n\)
26. Simplify: 162 × 82.
A. 210
B. 214
C. 215
D. 216
27. Simplify: 4a - 9b - 2(2a - 3b).
A. 8a + 3b
B. 8a - 3b
C. -15b
D. -3b
28. If \(\textbf{u} = \pmatrix{3 \\ 1}\) and \(\textbf{v} = \pmatrix{-2 \\ 1}\) evaluate \(6\textbf{v} + 2\textbf{u}\).
A. \(\pmatrix{-1 \\ 3}\)
B. \(\pmatrix{-6 \\ 8}\)
C. \(\pmatrix{1 \\ 3}\)
D. \(\pmatrix{6 \\ 8}\)
29. Find the image of the point (2, 5) under the transformation: \(\pmatrix{x \\ y} \to \pmatrix{x \\ 2 - y}\).
A. (2, –3)
B. (2, 2)
C. (2, 3)
D. (2, 7)
30. Find the image of Q(–4, 5) when rotated anticlockwise through 90° about the origin.
A. Q(−5, 4)
B. Q(−5, −4)
C. (4, −5)
D. (4, 5)
The following data show the marks of students in a test:
10, 4, 1, 4, 3, 3, 2, 1, 1, 7, 8
Use the information to answer questions 31 and 32.
31. If the pass mark is 4, find the number of students who scored more than the pass mark.
A. 1
B. 2
C. 3
D. 4
32. Find the mean mark.
A. 3
B. 4
C. 7
D. 8
33. How many lines of symmetry has a rhombus?
A. 2
B. 3
C. 4
D. 5
34. In an enlargement length AB = 3 cm and the length of its image A1B1 = 15 cm. Calculate the scale factor.
A. \(\frac15\)
B. \(\frac23\)
C. 5
D. 12
35. Find the rule of the mapping:
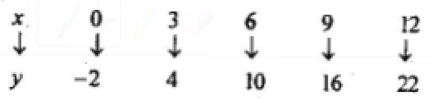
A. \(y \to \frac{x}{2} - 2\)
B. \(y \to x - 2\)
C. \(y \to x^2 - 2\)
D. \(y \to 2x - 2\)
36. Solve the inequality: \(\frac12(3x - 1) + 1 \leq 7 + 2x\).
A. x ≥ -14
B. x ≤ -14
C. x ≥ -13
D. x ≤ -13
37. If 4 - x = 3(4x + 5), find the value of x.
A. \(\frac{11}{13}\)
B. \(1\frac{6}{13}\)
C. \(-1\frac{6}{13}\)
D. \(-\frac{11}{13}\)
38. In class, there are 12 girls and 48 boys. Find the percentage of boys in the class.
A. 20%
B. 40%
C. 60%
D. 80%
39. The bearing of P from Q is 060°. Find the bearing of Q from P.
A. 120°
B. 150°
C. 210°
D. 240°
40. Which of the following statements best describes the construction below?
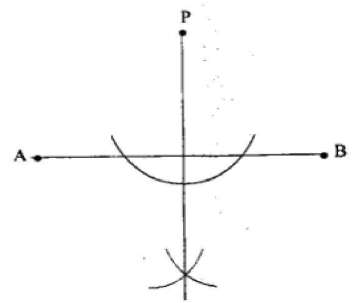
A. construction of line AB from P.
B. construction of perpendicular from P to meet line AB.
C. construction of an arc of a circle with centre P.
D. construction of the bisector of line AB.